 |
|
 |
| |
|
|
|
|
|
 |
|
 |
|
 QUANTITATIVE TECHNIQUE FOR MANAGEMENT QUANTITATIVE TECHNIQUE FOR MANAGEMENT |
|
|
|
|
| |
Hello student`s
Welcome to our Institute. We are here to provide you a Questions Papers for Year 2008 , 2009 and 2011
YEAR-2008 M.B.A-I semester
Time:3 Hours
Total Marks:-70
The Questions paper is divided into three sections.Sections A contains 10 questions of 02 Marks each. All questions are compulsory.
Section B will contain 05 questions of 10 marks each. The candidate are required to answer three questions from this section.
Section C is of 20 Marks and contains case studies or numerical problems only. Question for 40 marks are given in this section.
SECTION-A
Q.1 What is the role of models in business and industry?
Q.2 What is an optimal solution?
Q.3 Explain when to use the various decision criteria?
Q.4 What do you understand by degeneracy in Simplex?
Q.5 What is decision tree?
Q.6 What is the importance of normal distribution?.
Q.7 What does regression coefficient indicate? Is it possible that one coefficient has a positive value whereas the other happen
to be negative? If not why?
Q.8 What are the practical applications of correlation co-efficient?
Q.9 What are quantitative techniques?
Q10 What is the expected value of perfect information?
SECTION-B
Q11 An auotmobile company uses three types of steel S1, S2 ,S3 for producing
three different types of cars C1, C2 , C3. Steel requirement (in tons) for each
type of car and total available steel of all three types are summarized in following table:
| Types of steel | Type of Car
C1 C2 C3 |
Total Steel
Available |
| S1 | 2 3 4 |
29 |
| S2 | 1 1 2 |
13 |
| S3 | 3 2
1 |
16 |
Using matrix algebra determines the number of cars of each type which can be produced
Q12 Table below gives the data relating to purchase and sales. Obtain the two regression equations and estimate the
sales when the purchases equal to 65.
| Purchases | 57 | 58 | 59 | 59 | 60 |
61 | 62 | 64 |
| Sales | 77 | 78 | 75 | 78 | 82 |
82 | 79 | 81 |
Q13 Given the following input-output table, calculate the gross output so as to meet the final demand of 200
units of Agriculture and 800 units of industry:
| Producer Sector | Consumer Sector | Final Demand | Total Output |
| Agriculture | Industry |
| Agriculture | 300 | 600 | 100 | 1000 |
| Industry | 400 | 1200 | 400 | 2000 |
Q14 A newspaper boy has the following probability of selling a magazine:
| No.of Copies Sold | 10 | 11 | 12 | 13 | 14 |
| Probability | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 |
Cost of a copy is Rs.1.50 and selling price is Rs.2. He cannot return the unsold copies. How many copies should
he order? Also find EVPI
Q15 For the game having the following payoff table, use the graphical procedure to determine the value of the game
and the optimal mixed strategy for each player according to the minimax criterion.
| | Player 2 |
| Strategy | 1 | 2 | 3 |
| 1 | 1 | -1 | 3 |
| Player1 2 | 0 | 4 | 1 |
| 3 | 3 | -2 | 5 |
| 4 | -3 | 6 | -2 |
SECTION-C
Q.16 A manufacturing firm has discontinued production of a certain unprofitable product-line. This created considerable
excess production capactiy. Management is considering devoting this excess capacity to one or more of the 3 products;
P1, P2, P3. This available capacity on the machines which might limit output
is summarized in the following table:
| Machine Type | Available Time in Hours |
| Milling Machine | 200 |
| Lather | 100 |
| Grinder | 50 |
The number of machines hours required for each unit of the respective products is given below:
| Machine Type | Product P1 | Product P2 | Product P3 |
| Milling Machine | 8 | 2 | 3 |
| Lather | 4 | 3 | - |
| Grinder | 2 | - | 1 |
The sales deparment indicates that the sales potential for products P1and P2 exceeds the
maximum production rate and that the sales potential for product P3 is 20 per week. The unit profit would
be Rs.20, Rs 6 and Rs.8 respectively on products P1, P2 and P3
Formulates LP model for determining how much of each product the firm should produce in order to maximize
profit and solve.
Q.16) A supplier of machined parts has got an order to supply piston rods to a big car manufacture. The client has specified
that the rod diameter should lie between 2.541 and 2.548cms. Accordingly the supplier has been looking for the right kind
machine. He has identified two machines, both of which can produce a mean diameter of 2.545cms and the diameter
of the piston rods produced by both machines follows normal distribution. Like any other machines these machines
are also not perfect. The standard deviation of the diameters produced from the machine 1 and 2 are 0.003 and 0.005
respectively, i.e., machine 1 is better than machine 2. The cost of machine 1 is Rs.3.3 lakhs more than machine 2.
The supplier is confident of making profit of Rs.100 per piston rods; however, a rod rejected means a loss of Rs. 40.
The supplier wants to know whether he should go for the better machine at an extra cost.
YEAR-2009
Time: 3Hours
Total Marks: 70
This Question paper is divided in two sections. Section A contains 6 questions out of which the candidate is required to attempt any
4 questions. Section B contains short case study/application based one question which is compulsory. All questions are carrying equal marks.
SECTION-A
Q.1(a) Describe in brief some of the important quantitatives techniques used in modern business and industrial
units [7]
(b) Compute the inverse of the matrix. [7]
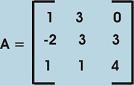
and hence find the solution of the following system of equations:
X - 2Y + Z = 0
3X + 3Y + Z = 7
0X + 3Y + 4Z = 7
Q.2 (a) The matrix of technological coefficients of input output in coal and iron industries is as follows:
| | Consumer Sector |
| Production Sector | | Coal | Iron |
| | Coal | 0.2 | 0.2 |
| | Iron | 0.6 | 0.2 |
If the final demand of coal and iron are 2400 tonnes and 800 tonnes respectively., Calculate the total production
of two industries [7]
(b) The incident of occupational disease in an industry is such that the workmen have a 20% chance of
suffering from it. What is the probability that out of six workmen, 4 or more will contract the disease?
[7]
Q.3(a) A firm manufacturing two types of electrical items, A and B, can make a profit Rs.20 per unit of A and Rs.30
per unit of B. Each unit of A requires 3 motors and 2 transformers and each unit of B requires 2 motors and 4
transformers. The total supply of these per month is restricted to 210 motors and 300 transformers. Type B
is an expert model requiring a voltage stabilizer, which has a supply restricted to 65 units per month. Formulate
above as a Linear programming problem for maximum profit and solve it graphically. [7]
(b) Solve the L.P.P by simplex method:
Max. Z = - x1 - x2
S.to 3x1 + 2x2 ≥ 30
-2x1 + 3x2 ≤ -30
x1 + x2 ≤ 5
x1 , x2 ≥ 0
Q.4(a) Three coins are tossed simultaneously. Find the probability of:
(i) all heads
(ii) one head
(iii) atleast one head
(iv) all tails [7]
(b) From the following data calculate coefficient of correlation between X and Y series by square of values method:
| X | 7 | 8 | 10 | 11 | 9 | 5 | 6 | 2 |
3 | 6 |
| Y | 10 | 12 | 8 | 2 | 4 | 3 | 5 | 2 |
4 | 7 |
Q.5(a) What do you understand by decision-making with imperfect information? Explain the decision theory in short
, with reference to experimental approach [7]
(b) The manager of a flower shop promises its customers delivery within four hours on all flower orders. All flowers are
purchased on the previous day and delivered to parper by 8.00 A.M. the next morning. The daily demand for roses is as
follows:
| Dozen of roses | 70 | 80 | 90 | 100 |
| Probability | 0.1 | 0.2 | 0.4 | 0.3 |
The manager purchases roses for Rs.10 per dozen and deals them for Rs.30. All unsold roses are donated to a local
hospital. How many dozens of roses should parper order each evening to maximize its profit? What is the optimum
expected profit? [7]
Q.6(a) Explain the theory of dominance in the solution of rectangular game. [7]
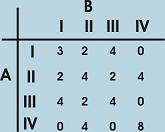
(b) Solve the game whose pay off matrix is given by, [7]
SECTION-B
Q.7(a) Solve by Simplex Method: [7]
Max. Z = 4x1 + 3x2
S.to 2x1 + x2 ≤ 30
x1 + 2x2 ≤ 24
And
x1 ≥0, x2 ≥0
(b) Use two phases simplex method to solve the problem [7]
Min Z = 15/2x1 - 3x2 + 0x3
S.to 3x1- x2 - x3 ≥ 3
x1 - x2 + x3 ≥ 2
x1 ≥ 0 , x2 ≥ 0, x3 ≥ 0
YEAR-2011
Time: 3Hours
Total Marks: 70
This Question paper is divided in two sections. Section A contains 6 questions out of which the candidate is required to attempt any
4 questions. Section B contains short case study/application based one question which is compulsory. All questions are carrying equal marks.
SECTION-A
Q.1 (a) " Model building is the essence of decision making". Explain
(b) A manufacturer is manufacturing two types of products X and Y. M1 and M2 are two machines which are used to manufactures these products. The time taken both by X and Y on machines is given below:
| | M1 | M2 |
| Product X | 20 hours | 10 hours |
| Product Y | 10 hours | 20 hours |
If 600 hours is the time available on each machine, calculate the number of units of each type manufactured using matrix only. [6+8]
Q.2 (a) When does a Binomial distribution tend to become a normal and poisson distribution?
(b) A leading razor blade manufacturing factory turns out razor blades with a small chance of one out of 1000 blades to be defective.Blades are supplies in packets of 10. Using Poisson approximation, calculate the approximate number of packets withour any defective blades and with one defective in a consignment of 1,000 packets. [7+7]
Q.3 (a) A firm makes two types of furniture - chairs and tables. The contribution for each product as calculated by the accounting department is Rs 20/- per chair and Rs. 30/- per table. Both products are processed on three machines M1,M2 and M3. The time required in hours by each product and total time available in hours per week on each machine are as follows:
| Machine | Chair | Table | Available Time |
| M1 | 3 | 3 | 36 |
| M2 | 5 | 2 | 50 |
| M3 | 2 | 6 | 60 |
How should the manufacturer schedule his production in order to maximize contribution?
(b) Explain the limitations of linear programming. [8+6]
Q.4 (a) Two students A and B are given the same problem to solve. The odds in favour of A solving the problems are 4 to 6 while against B solving the problem are 6 to 5. Both the students try to solve the problem. Find the probability of the problems being solved.
(b) The competitors in a beauty contest are ranked by three judges in the following order :
| First Judge | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
| Second Judge | 3 | 5 | 8 | 4 | 7 | 10 | 2 | 1 | 6 | 9 |
| Third Judge | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
Use the rank correlation to discuss which pair of judges have the nearest approach.
[6+8]
Q.5 (a) What do you mean by Statistical Decision Theory? What is the difference between decisoin making under uncertainity and risk? Prepare conditional profit and conditional opportunity loss tables by taking imaginary figures.
(b) Solve the following two person zero-sum game:
[8+6]
| Player B |
| | - | B1 | B2 | B3 |
| | A1 | 5 | 7 | 11 |
| Player A | A2 | 2 | -1 | 8 |
| | A3 | 18 | -6 | 10 |
Q.6 (a) Write short notes on the following :
(i) Sadde Point
(ii) Pay-off matirx
(iii) Concept of Dominance
(b) In order to study the productivity of workers in an industry, ten workers were selected at random and their score on apptitute test and the productivity indices were compiled :
| Appitute Score(X) | 60 | 62 | 65 | 70 | 72 | 48 |
53 | 73 | 65 | 82 |
| Productivity Index(Y) | 68 | 60 | 62 | 80 | 85 | 40 |
52 | 62 | 60 | 81 |
From these details, estimate the productivity index for a worker whose test score is 75 [6+8]
SECTION-B
Q.7 (a) Solve the following game by linear programming.
| | B1 | B2 | B3 |
| A1 | 1 | -2 | 1 |
| A2 | -1 | 3 | -2 |
| A3 | -1 | -2 | 3 |
(b) A producer of boats has estimated the following distribution of demand for a particular kind of boat.
| No.of demand | 0 | 1 | 2 | 3 | 4 | 5 |
6 |
| Probability | 0.14 | 0.27 | 0.27 | 0.18 | 0.09 | 0.04 |
0.01 |
Each boat costs him Rs.7,000 and he sells them for Rs.10,000 each. Any boat that is left unsold at the end of season must be disposed off for Rs.6,000 each. How many boats should be in stock so as to maximize his expected profit?
[7+7]
|
|
 |
|
 |
|
|
|
|
 |
|
 |
|